Treatment of Potential Queue-Up Situations

For all bridge claims with the potential of having two bridges queue up after one another (mentioned in the example cases above), the following rule applies:

The acceleration rate (a), maximum speed (s) and deceleration rate (d) of the following bridge (F) are compared with the a, s, and d of the leading bridge (L). If all of the following conditions are true, bridge F moves independent of bridge L.

Conditions for No Queue-Up

1. aF <= aL The following bridge cannot accelerate faster than the leading bridge.

2. sF <= sL The following bridge’s maximum speed cannot be greater than the leading bridge.

3. dF >= dL The following bridge can decelerate equally or faster than the leading bridge.

If any one of the above conditions fail, bridge F moves at the same speed as bridge L, maintaining the distance that existed between them at the time F started moving.

Please note

Condition 3 usually creates a deviation from the typical real life situation, but it is necessary to avoid time consuming computations that can adversely affect the run-time performance of models with crane resources. To avoid unrealistic queue-ups when modeling multiple bridges with different mobility characteristics in the same crane envelope, make either no bridge deceleration entry (infinite deceleration), or use the same overall average deceleration rate for all crane bridges in that envelope.

Bridge Motion after Queue-Up

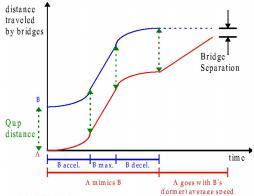
If bridge A is queued up behind bridge B, bridge A goes through up to two stages of movement. The first stage occurs throughout the movement of bridge B. Bridge A mimics bridge B’s motion, maintaining its original distance from bridge B.

The second stage occurs after bridge B stops. Bridge A continues traveling with the former average speed of bridge B until it reaches its destination.

If bridge B is moving to accomplish its own task (as opposed to just moving out of A’s zone), then bridge A might stop earlier, without going through the second stage. In this case, the total traveling time for bridge A is calculated as if bridge A were traveling with bridge B’s average speed.

When a bridge arrives at its destination, it triggers a chain queue-up re-evaluation that penetrates the crane envelope in the opposite direction that the stopped bridge was moving. This chain re-evaluation handles cases in which there were multiple bridges queued up behind the stopped bridge.